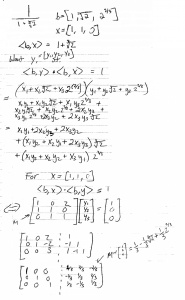It’s been awhile since I blogged, so I thought I’d take a moment to talk about couple interesting math problems that came up in a conversation I, @SuburbanLion, had on Twitter with @MathGuide, @RepublicOfMath, and @GMichaelGuy about a month ago. The topic of discussion was the role of rationalization problems in Algebra II and whether or not the current curriculum addresses the “conceptual core” of these problems.
A common example that one would see in an Algebra II course is:
- Rationalize the denominator of
![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{2}}\]](https://suburbanlion.com/wp-content/ql-cache/quicklatex.com-89b5b9cf87b9809df8ff6b0076ebf247_l3.png)
Or simply:
- Rationalize
![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{2}}\]](https://suburbanlion.com/wp-content/ql-cache/quicklatex.com-89b5b9cf87b9809df8ff6b0076ebf247_l3.png)
The expected answer for this problem can be obtained by multiplying the numerator and denominator both by
![]()
to get:
![]()
. Students might be assigned dozens of such problems in Algebra II. The question to be asking is “Why?”.
I suspect that the obvious answer is historical tradition. These math problems have been passed down from generation to generation as “standard Algebra II problems”, and even the new Core Standards includes “rewrite expressions using radicals and rational exponents” as an objective. Instead of treating these problems as a “means to an end”, these problems have become something of an end in themselves. Algebra II students learn to rationalize expressions because that’s what they’re going to be tested on. End of story.
The real reason for having these problems in Algebra II goes deeper than that. The Core Standards hits on this reason (at least partially) with one of the additional objectives: “Understand that rational expressions form a system analogous to the rational numbers, closed under addition, subtraction, and division by a nonzero rational expression.” While this objective is not specifically talking about radical expressions, the core concept is the same. More concisely, we might say that the important point of rationalizing radical expressions is to come to the conclusion that
![]()
is a field.
Ironically, the 93 page Core Standards does not even mention the word “field” even though this is essentially the core concept that students are learning about. Students shouldn’t be rationalizing expressions just for the sake of rationalizing expressions, they should be exploring the intermediate steps between the field of rational numbers and the field of algebraic numbers. By the way, the phrase “algebraic number” doesn’t appear in the Core Standards either!
To make things interesting, G. Michael Guy presented a couple rationalization problems that are typically not included in Algebra II problem sets. These are actually really great examples of the potential complexity involved in rationalization problems.
Let’s warm up with the first one, which is significantly easier:
- Rationalize
![Rendered by QuickLaTeX.com \[\frac{1}{1+\sqrt[3]{2}}\]](https://suburbanlion.com/wp-content/ql-cache/quicklatex.com-393e7e6e951c5a8fa32010d0ad05833c_l3.png)
This one has an elegantly simple solution using the sum of cubes factorization:
Making the substitutions a = 1, b =
![]()
, we can take advantage of this product to rationalize the denominator:
This solution is simple enough that this could almost pass for an Algebra II problem. Rationalization problems in Algebra II are something of a gimmick: the problems chosen are special cases designed to have an easy answer. The methods taught in the textbook will solve the given problems, but they don’t generalize well to the larger class of problems. The techniques used in Algebra II provide very little help in rationalizing an expression like
![]()
!
Before we attempt something like this, lets go back to
![]()
and come up with a method that will generalize well. This is where easy problems come in handy as a test bed for discovering the broader patterns. The general case of rationalizing
![]()
can be reasonably done by hand.
The method used here is not likely to be seen in a typical Algebra II classroom, as it relies on concepts from Linear Algebra which typically aren’t addressed until later. Seems a little backwards if you ask me. The trick here is to think of the product
![]()
as the product of a matrix and a vector:
Solving this equation is then simply a matter of multiplying both sides by
![]()
. This method extends nicely to even harder problems, including
![]()
. Inverting a 27 by 27 matrix is not something I’d want to be doing by hand, so this is where computers come in handy. Here’s an algorithm for rationalizing
![]()
in Sage. Compare this with Wolfram|Alpha’s result.
I’m a strong believer that computing should play a larger role in mathematics education than it is presently. Not only should the curriculum be addressing the fact that the algebraic numbers form a field, but also that all algebraic numbers are computable numbers. By shifting the focus of discussion from solving problems to finding an algorithm for solving those problems, we can reveal a better picture of the mathematics behind the problem. Simple problems worked out by hand play an important role in the process of designing an algorithm, but an ability to generalize the solution should be the larger goal. If the rationalization problems that students are completing by the dozens do not lead the student in the direction of a general solution, then those problems are not doing their job. Perhaps some “harder” problems are necessary to encourage that generalization.
For the record, “computable numbers” are not referenced once in the Core Standards. It’s hard to give students a 21st century education when the math curriculum is trapped in the early 1900s.

![Rendered by QuickLaTeX.com \[\frac{1}{1+\sqrt[3]{2}}\cdot\frac{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}}{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}} = \frac{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}}{1+\sqrt[3]{2}^{3}} = \frac{1-\sqrt[3]{2}+\sqrt[3]{2}^{2}}{3}\]](https://suburbanlion.com/wp-content/ql-cache/quicklatex.com-f4820e1ae425c7c75b874f4cf303c55b_l3.png)